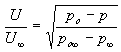
Experiments 3 and 4 involve the study of flow past a circular cylinder in a uniform stream. In Experiment 3 this is done in a wind tunnel using conventional instrumentation, specifically a Pitot static probe and static pressure ports. In Experiment 4 this is done in a water tunnel using a state-of-the-art instrumentation known as Particle Shadow Velocimetry. The objective here is to give you experience of the broad range of flow measurement technology that is available to the aerospace or ocean engineer. You will also observe, in practice, a flow you have met only in theory up to now.
The flow past a two-dimensional cylinder is one of the most studied of aerodynamics. It is relevant to many engineering applications. The flow pattern and the drag on a cylinder are functions of the Reynolds number ReD = U∞D/n, based on the cylinder diameter D and the undisturbed free-stream velocity U∞. Recall that the Reynolds number represents the ratio of inertial to viscous forces in the flow. The drag is usually expressed as a coefficient C d = d/(½ρU∞2D), where d is the drag force per unit span.
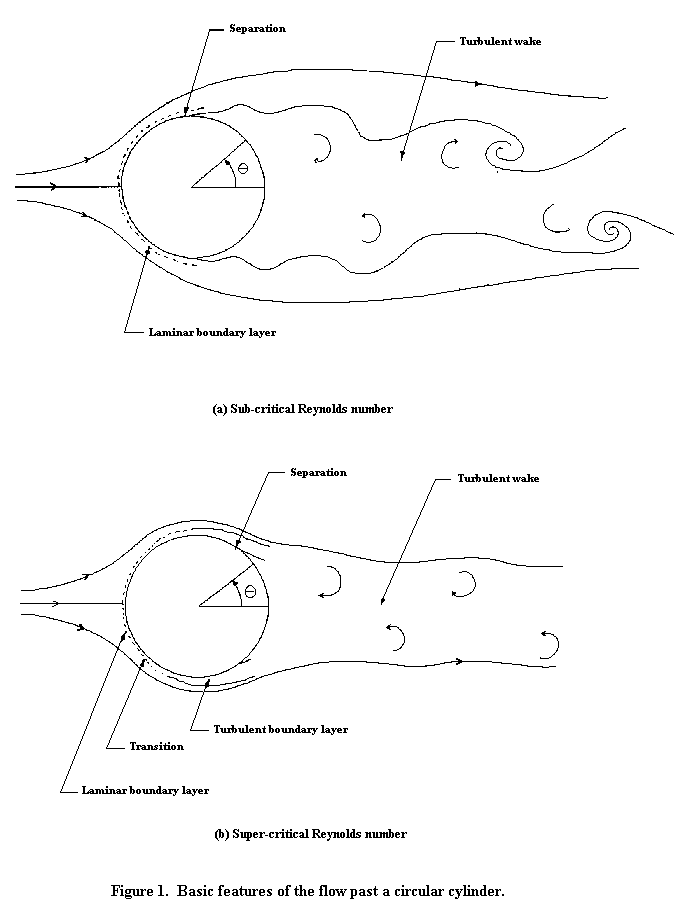
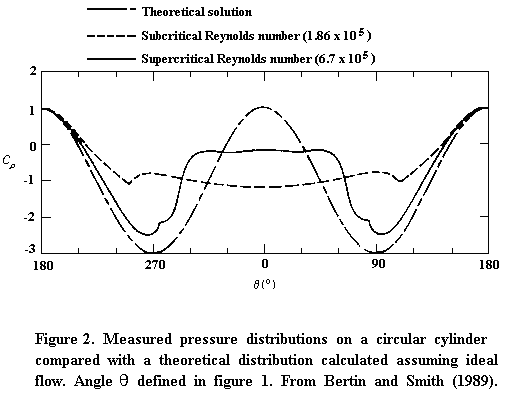
The flow pattern at high Reynolds numbers (ReD > 10000) is sketched in Figures 1(a) and 1(b) . At the leading edge of the cylinder a stagnation point is formed where the oncoming flow is brought to rest. The pressure here is equal to the stagnation pressure. The pressure coefficient Cp = (p - p∞)/(½ρU∞2) there is therefore equal to 1 by Bernoulli's equation (see Figure 2 from Bertin and Smith, 1989). To either side of the stagnation point the flow accelerates around the forward surface of the cylinder producing a drop in the pressure (Figure 2). Immediately adjacent to the cylinder surface a thin boundary layer is formed. The boundary layer is a region where the velocity drops rapidly to zero to satisfy the no slip condition at the cylinder surface. The direct effects of viscosity are felt only within the boundary layer.
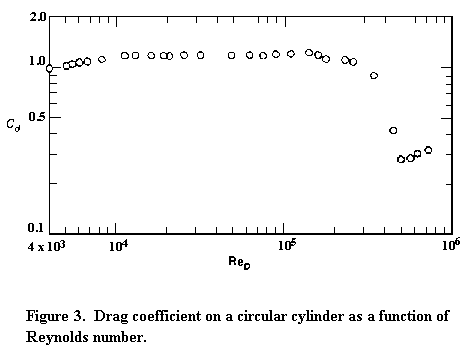
If ReD is less than about 400,000 the boundary layer remains laminar from the stagnation point at the front of the cylinder to the point where it separates. The resulting flow pattern (Figure 1(a)), termed sub-critical, is associated with a high drag on the cylinder (see Figure 3 from Bertin and Smith, 1989), Cd being about 1.2. The laminar boundary layer separates just upstream of the maximum thickness (see Figure 1(a)). Separation occurs because the boundary layer anticipates the deceleration of the flow (and therefore positive pressure gradient) that would otherwise occur on the rearward face of the cylinder. Downstream of separation the flow quickly becomes turbulent and a broad wake is formed. The wake as a whole is unstable and rolls up into vortices that are shed antisymmetrically at regular intervals from the cylinder (Figure 1(a)). This type of wake is called a von Kármán vortex street (see for example, von Kármán (1963)). Because of separation the pressure remains low and approximately constant over the rearward face of the cylinder. This causes a net imbalance of pressure forces on the cylinder (Figure 2), usually referred to as the pressure drag. Pressure drag accounts for about 90% of the total drag on the cylinder in this regime. The remaining 10% is due to skin-friction drag - friction between the flow and the cylinder. Most skin-friction drag is produced on the forward-face of the cylinder where the boundary layer is thin and velocity gradients at the cylinder surface are large.
At Reynolds numbers greater than about 400,000 the boundary layer on the forward face of the cylinder undergoes transition and becomes turbulent. The resulting flow pattern (Figure 1(b)), termed super-critical, is associated with a much lower drag, Cd being about 0.3. The precipitous drop in Cd that occurs as a result of transition is usually referred to as the drag crisis. The turbulent boundary layer generated in super-critical flow is much less susceptible to adverse pressure gradients. It remains attached to the cylinder surface well past its maximum thickness. As a result the wake is much narrower, the imbalance of pressure forces on the cylinder surface is much smaller and the pressure drag is greatly reduced. This reduction swamps a small increase in skin-friction drag produced by the greater length of the boundary layer and its transition. Note that the drag crisis need not always occur at ReD = 400,000. Roughness of the cylinder surface or unsteadiness in the free stream (such as is present in the open jet wind tunnel) can cause boundary layer transition at much lower Reynolds number.
The above is a brief and truncated description of the structure of the flow past a cylinder. This flow is both complex and beautiful. If you are interested further consult Bertin (2001), Panton (1984), van Dyke (1982) and, perhaps, your own flow visualizations from Experiment 1 or Experiment 4 if you have done them yet.
As you will see later on in Experiment 7, it is rarely possible to match the full scale conditions in the wind tunnel. As you know, the equations of fluid dynamics depend on a series of non-dimensional quantities, the most important of which are the Reynolds number Re (that indicates the importance of viscous effects) and the Mach number M (related to compressibility effects). Ideally, a wind tunnel test at the same Re and M experienced by a full scale vehicle would have the same flow (ignoring the effects of the walls and any imperfections). In most circumstances this can't be done:
In experiment 3 you will have the opportunity to investigate for yourself
the flow past a cylinder over a range of Reynolds numbers. You will have
a wind tunnel, model and equipment for measuring pressure and velocity
at your disposal. Through analysis these measurements can be used also
to estimate the drag on the cylinder and the shape of its wake.
A. Instrumentation for measuring the properties of the air.
The open jet wind tunnel used in this experiment uses the laboratory
atmosphere as the working fluid. The properties of the air in the lab vary
depending on the weather so it is important that you measure them, so you
know what fluid you are working with. From the point of view of the dynamics
of the air, the important properties are its density and viscosity (think
of Bernoulli's equation and the Reynolds number).
Rather than measuring density directly, it is best obtained by measuring pressure and temperature and then using the equation of state for a perfect gas. There are different ways of obtaining atmospheric pressure for experiments. For example:
Although there is a temperature sensor on the SenseHat, an additional temperature probe is use for better accuracy. The DS18B20 1-wire digital temperature probe is connected to the Raspberry Pi having an uncertainty of ±0.5 deg C. The temperature probe is located on the side of the open-jet tunnel next to the test section. Both atmospheric pressure and temperature can be recorded during data acquisition process using a Matlab GUI code. A computer will be available for the data acquisition. The gas constant R in the equation of state for a perfect gas (p =ρRT) is 287 J/kg/K.
The temperature can also be used to infer the dynamic viscosity of the air using Sutherland's relation. For SI units,
where T is temperature in Kelvin. Recall that kinematic viscosity ν is dynamic viscosity divided by density. You can program Sutherland's relation in your electronic logbook, or use the calculator below:
B. Open jet wind-tunnel model and circular cylinder model
The experiment will be performed in the 0.7m subsonic open jet wind tunnel,
a detailed description of which is given in Appendix
2 . Mounted in the wind tunnel is the cylinder model. The model is
built from Plexiglas. It has a diameter D of 140mm and a span of 462mm.
Circular end plates of diameter 305mm are used to minimize flow around
the ends of the cylinder. These plates act to make the flow more two dimensional
(though how two-dimensional is open to question). The cylinder model is
mounted spanwise across the test section. The mount allows the cylinder
to be rotated about its axis by a measured angle (indicated by the attached
protractor). It also allows the cylinder to be placed at different streamwise
positions. For the purposed of this experiment, the cylinder will be placed with its axis at 25 cm
downstream of the contraction exit.
The freestream velocity is monitored using pressure taps located at the exit of the settling chamber. These taps are connected to a pressure scanner located next to the wind tunnel. Since the pressure scanner is reading the difference between pressure at the end of the line to the atmospheric pressure, the settling chamber static pressure can be computed for the flow velocity coming out of the contraction, using Bernoulli's equation, po = p + ½ρU2.
The bulk of the pressure measurements will be performed with the Esterline 9816/98RK pressure scanner. This instrument has 48 channels with a range of +/-10 inches of water column. The system has a rated accuracy of +/-0.05% full scale. This pressure scanner is a transducer that can measure up to 48 different pressures simultaneously. In other words, while one could try to measure the pressure from each port on the circular cylinder described in Part C with a single digital manometer, the same measurement of the 36 pressure ports can be performed in less than 10 seconds with the scanner. Such capability should allow for a wide variety of measurements to be performed during your experiment. The pressure scanner should be connected as follows:
To sense this pressure difference, and thus the free stream velocity, the probe is connected through two Tygon tubes to an Esterline 9816/98RK pressure scanner, that can measure pressures in inches of water column (the height of water column h is related to pressure through the hydrostatic equation p=ρwatergh). The pressure tube system (indeed any pressure tube system) will not work unless it is sealed. With the tunnel off you should check that the scanner reads zero (the "Calibrate Scanner" button in the Matlab program will adjust the initial reading to zero if necessary).
The pressure scanner is controlled by a computer through the same Matlab GUI used for the atmospheric pressure and temperature reading. This code allows you to visualize the pressure around the cylinder (much like an old analog multi-tube manometer would) and save the corresponding data. A description of the pressure scanner and the Matlab GUI used to control it can be found in Appendix 2. Make sure to read the scanner manual to understand how the control program works. The scanner is an Ethernet based system that connects to the acquisition computer using a RJ-45 cable (ethernet cable). Once logged on to the computer, open Matlab and browse to C:\AOE3054 - Open Jet Pressure Scanner\. Once in this folder, ensure both the traverse and scanner are turned on and then run acquirePressureScanner.m. You should be able to confirm the scanner is connected correctly by traversing the downstream Pitot-static probe while the flow is on, and observing how the distribution changes on the Matlab plot.
In addition to the above items the wind tunnel facility is equipped with a Pan-Tilt-Zoom camera system, which you can use to document the various setups and instrumentation you use. The camera has 2x optical and 16x digital zooming capability so can be used to observe detailed motion inside the test section. The cameras are managed by Milestone XProtect, a video management software, that allows for the remote operation of both cameras in pan, tilt, and zoom. For an in-person option, several measuring instruments (tape measure, steel ruler, caliper) are also available and can be used to measure the model, its placement and the placement of the probes.
This will be a good time to start your electronic logbook, measure and record atmospheric pressures, model dimensions, take and record photos of the various equipment noting, as always, your quantitative impression of the accuracy of those measurements.
C. Instrumentation for measuring the pressure distribution on the
cylinder surface
Depending on the goals you choose for your measurement you will probably
need to measure the surface pressure distribution on the circular cylinder
or, more specifically, the distribution of surface pressure coefficient.
The pressure coefficient is defined as
with p representing the pressure at the cylinder surface, the other symbols being defined above. Note that the denominator of the pressure coefficient p - p∞ is what is already being measured by the reference Pitot-static system.
The cylinder is instrumented with 36 one-millimeter diameter pressure taps at 10 degree intervals, around its circumference at mid span. These sense the surface pressure p and transmit it through a series of 3mm outside diameter Tygon tubes to the outside world. The distribution of p is measured using an Esterline pressure scanner. This system can measure the pressure on all 36 ports simultaneously. Initially all the Tygon tubes are connected to tthis in a clockwise order with channel 1 as the foremost port - ask your lab instructor to help rotate the cylinder if not in the correct order. A description of the pressure scanner and the Matlab code can be found in Appendix 2 . The pressure from the Matlab code is given in inches of water column. The pressure p (relative to atmospheric) can be obtained using the hydrostatic equation
To form the numerator of the pressure coefficient it is then necessary to measure p∞ relative to atmospheric and subtract it from these readings.
The Matlab code provides an easily understood way of simultaneously visualizing the pressure distribution on the entire circumference of the circular surface. It also saves the data in a user-defined file that can be used to re-plot the distribution for further analysis.
D. Instrumentation for measuring the cylinder wake
A three-axis computer-controlled traverse gear, described in Appendix
2 is mounted towards the back of the wind tunnel test section. Mounted
in the traverse gear is a Dwyer model 160 Pitot-static probe. Tygon
tubes are provided to transmit the pressures sensed by the Pitot-static
out of the test section.
The Dwyer model 160 Pitot-static probe is mounted towards the back of the test section.
This probe monitors the velocity and pressure downstream of the cylinder. There are two pressure connections to the probe.
The one on the axis is connected to the Pitot, or stagnation, port and thus registers the stagnation pressure of the free stream po∞,
the pressure produced by bringing the flow to a halt at the mouth of the tube.
The tube on the side of the probe is connected to the static ports on the side of the probe and thus registers the static
(i.e. actual) pressure of the free stream p∞.
The difference in these pressures is related to the local velocity through Bernoulli's equation, po - p = ½ρU2.
To sense this pressure difference, and thus the local velocity, the probe is connected through two Tygon tubes to the Esterline 9816/98RK pressure scanner similar to the cylinder surface pressure. Scales attached to the longitudinal, horizontal and vertical axes of the traverse allow the relative position of the Pitot probe in the cross plane. If you use this probe you will have to use the observe the distance of the probe tip to the center of cylinder to determine its absolute position (both streamwise and in the cross plane) relative to the cylinder.
The most obvious quantity that can be measured with this Pitot-static probe is the velocity distribution in the cylinder wake. If p o and p represent the Pitot and static pressure sensed by the probe then the local velocity is given by Bernoulli's equation po - p = ½ρU2, and (more importantly) the ratio of the local velocity to the free stream velocity is given by
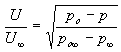
Determining this ratio is thus a matter of using the second digital manometer to determine the difference between the stagnation and static pressure for the Pitot static probe on the traverse, dividing by the (simultaneously measured) pressure from the reference manometer, and then taking the square root of the result.
Another quantity that can be measured using the traversing Pitot-static probe is the stagnation pressure po which is normally expressed using the total pressure coefficient
As you know from AOE 3014, the stagnation pressure in inviscid steady flow remains constant, and equal to its free stream value. As you can see, the stagnation pressure coefficient will remain 1 in this case. The stagnation pressure always drops as a result of viscous effects such as are encountered inside the edge of a turbulent wake, like that shed by the cylinder, and thus here the stagnation pressure coefficient will always be less than 1. This property of the stagnation pressure coefficient makes it a very good indicator of the edge and extent of a wake. For example, a reasonable definition of the wake edge would be the point where Cpo falls to 0.98.
One interesting aspect of using the Pitot-static deep inside the cylinder
wake is that the flow here contains regions of flow reversal and high turbulence
where the validity of this technique may be brought into question (refer
back to your class notes on velocity and pressure measurement techniques).
You can therefore also use this set up to see what happens to a Pitot static
measurement in such a region.
B. Determining the pressure drag from surface-pressure measurements
The drag on a real cylinder is, of course, not zero and can be estimated
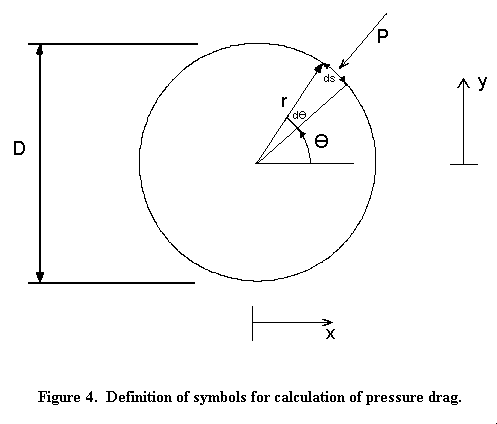
from a measured pressure distribution as follows. Consider an element of
the cylinder surface of length ds = rdθ
as shown in Figure 4 . The force per unit span on the
element due to a pressure normal to the element is
![]()
The drag component of this force is the component acting in the direction of the free-stream velocity
![]()
The integral of this around the cylinder circumference gives the total drag on the cylinder per unit span d.
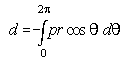
Now, it is conventional to work in terms of the non-dimensional drag coefficient and pressure coefficient, respectively:
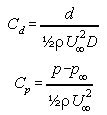
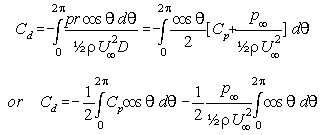
the second integral is zero, giving,
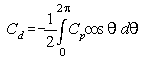
This integration can be done numerically using Simpson's or the trapezium rule or by plotting Cpcosθ vs. θ and measuring the area under the curve. Note that θ is measured in radians.
The above estimate of Cd takes account
only of the pressure drag on the cylinder. In calculating this, however,
it is fairly accurate, the main source of error probably being the numerical
integration.
A. Getting familiar with equipment
The following procedures are designed to help you
get a feel for the open jet tunnel, the cylinder model and the instrumentation.
It is important that each student get a hands on feel of how to use the apparatus
and what its capabilities and problems are. Feel free to play with the
apparatus at this stage, but don't forget to record any results, thoughts,
ideas or concerns in the logbook. Throughout the experiment you can ask for TA assistance using
the Press to Call TA button on the Matlab GUI.
Goal 1. Design, conduct, and implement a series of tests to determine the pressure distribution and drag coefficient on the circular cylinder at a fixed Reynolds number, and compare with inviscid theory.The group should leave few minutes at the end of the lab period for discussion and to check that everybody has everything they need. As a group go through the exit checklist.
Suggestions. Your drag estimate can be compared with data from Figure 3 . The pressure distributions could additionally be compared with the sub and supercritical experimental results in Figure 2 . Checking some pressure measurements, qualitatively or quantitatively, with an independent system (you have two) would provide assurance that they are about right. Analyze and plot your results as you go. Note and re-measure any funny looking points (keep both sets of measurements). Keep careful documentation of what you do, why you do it, set up characteristics, expected results, unexpected results, analysis, photos and plots in the electronic logbook as you proceed. You might be wise to check out the spanwise uniformity of the flow at one Reynolds number, using the traverse. Whether or not it is uniform may be an important thing to talk about when presenting your results in your report. Analysis should include uncertainty estimates for all results. This maybe a challenge for the drag estimate, but remember that integrating the drag is a lot like taking a average of many samples as is done in the class example on uncertainty.Goal 2. Design, conduct, and implement a series of tests to determine the shape and form of the circular cylinder wake at a fixed Reynolds number.
Suggestions. Imagine the wake as a three dimensional structure trailing behind the cylinder. Discuss in your group where you want to measure the location of the wake edge. Do you want to measure velocity (more easily discussed and related to theory) or stagnation pressure coefficient (more accurate for determining the wake edge)? Do you want to measure more than the wake edge, e.g. profiles across the wake, 2D cross section through the wake (you could plot contours of the measured quantity then), so you can see the behavior of the Pitot-static in the highly turbulent region near the wake center. Don't forget to try and characterize whether the probe is influencing the flow it is trying to measure, whether the wake is symmetric. Remember that thanks to the pressure scanner you can measure the cylinder pressure distribution while measuring the wake. If you have already measured the pressure distribution at the centerline, the wake shape here would be particularly important. Analyze and plot your results as you go. Re-measure any funny looking points. Keep careful documentation of what you do, why you do it, set up characteristics, expected results, unexpected results, analysis, photos and plots in the electronic logbook as you proceed. You might be wise to check out the spanwise uniformity of the flow at one Reynolds number, using the traverse. Whether or not it is uniform may be an important thing to talk about when presenting your results in your report. Analysis should include uncertainty estimates for all results.Goal 3. Find out the effect of Reynolds number on drag and/or pressure distribution and/or wake shape and compare with data from Figures 2 and 3 .
Suggestions. Three wisely chosen Reynolds numbers maybe enough. Remember the Reynolds numbers goes as the square root of the reference Pitot-static pressure. See suggestions under Goals 1 and 2. At this point you can also investigate the effects of a boundary layer trip or surface disturbance. Try various radius locations using the 0.85mm thick zigzag tape provided (your TA can assist in putting the tape when working remotely), or try various locations and sizes (you can start with a piece of tape and go to a piece of wire or yarn or sandpaper - discuss this in details with your TA or instructor prior to the lab and provide them with the material you want to use at least a day before the experiment). You will also need to coordinate with your TA as they will be the one installing it on the model. How does it impact the pressure distribution and/or the wake? How do your results compare to the theory presented in Figures 2 and 3.Goal 4. Find out if this cylinder model undergoes a drag crisis, and the Reynolds number or range of Reynolds numbers over which that occurs. Note that you won't be able to reach a Reynolds number of 400,000 with the open jet wind tunnel, but (as discussed at the end of Section 1) this may not be necessary with the free stream turbulence present in this facility.
Suggestions. When hunting through Reynolds numbers for the drag crisis, qualitative measurements of the surface pressure distribution on the cylinder may be enough to indicate the state of the flow. If you find a range of Reynolds numbers you should then start to worry (a) if it doesn't agree with Figure 3, why not? or (b) if it does agree with Figure 3, should it? Is the flow really 2D? symmetric? can you check it? is the tunnel quality an issue (Appendix 2)? You would be wise to firm up your conclusion that the flow is subcritical, and supercritical with at least some quantitative measurements. Keep careful documentation of what you do, why you do it, set up characteristics, expected results, unexpected results, analysis, photos and plots in the electronic logbook as you proceed. Analysis should include uncertainty estimates for all results. This maybe a challenge for any drag estimates, but remember that integrating the drag is a lot like taking a average of many samples as is done in the class example on uncertainty.Goal 5. Perform a calibration of the wind tunnel and determine its flow uniformity.
Suggestions. While this facility has been tested at various occasions, there is no formal calibration yet. If you chose, you can measure velocity cross-sections of the flow at various speeds and streamwise locations to determine flow uniformity. This would require removing the cylinder model and using only the Pitot-static probe mounted on the traverse (this is difficult to achieve for the online session and is not advised).
Before starting your report read carefully all the requirements in Appendix 1.
Title page
As detailed in Appendix
1 .
Introduction
Begin this section by stating logical objectives of the experiment
that best fit how your particular investigation turned out and what you
actually discovered.
In the second half of this section explain in summary form what was done to achieve these objectives (mention in broad terms what types of analysis were done as well as the experiment itself). A good start here is "To attain these objectives, experiments were....". The purpose of this is to tell the reader enough so that he or she knows what to expect in the rest of the report. Giving the reader "advance warning" like this makes the report much clearer and easier to read.
Follow this with a background to the technical area of the test and/or the techniques. This material can be drawn from the manual (no copying), classes or even better, other sources you have tracked down yourself. This could be a good place to describe the basis of the inviscid theory for flow past the cylinder. Finish with a summary of the layout of the rest of the report.
Apparatus and Instrumentation
In this section you need to describe each item of equipment and explain
how it was used. (If it helps, feel free to use a separate subsection for
each item.) Begin with the wind tunnel giving details that are relevant
to this experiment (e.g. closed circuit, contraction ratio, dimensions
and shape of test section, open jet test section, quality of flow (see
Appendix
2 ), speed range, reference Pitot-static used to monitor flow speed
and its set up, temperature monitoring, manometer characteristics and model
numbers etc.). Don't omit obvious things, e.g. the name of the wind tunnel.
Then describe the model. Important details are; its shape and dimensions,
how and where it was mounted, what it is made of, how it is instrumented
(including the manometer(s) and pressure scanner). Finally give the details of the Pitot-static
tube (size, shape, where and how it was mounted, traverse gear, how it
was used).
It is often much easier to describe clearly the size, shape and relative positions of objects if you include a diagram or dimensioned and labeled photo. A picture of some kind, with dimensions, of the test section showing the model, Pitot-static tube and reference Pitot- static is definitely needed. You could also put the coordinate system you are going to use later in presenting results on this figure, and describe it in the text (some suggested words for doing this can be found in the Recommended Report Format section of Experiment 4 ). Other diagrams or plots (some of which you may wish to copy from the manual) may make this section easier to write and read. Diagrams of tubing arrangements may help explain what you measured and why.
Uncertainties in primary measurements should be included in this section.
Results and Discussion
A good way to open this section is to briefly state what raw measurements
were made and at what conditions and why - the why should fit in with your
objectives (e.g. "Measurements of static pressure coefficient on the cylinder
surface were used to determine...").
Then introduce the plots (e.g. "Results are presented in figures ....") and then describe any variables and parameters used in them (e.g. "The coordinate system used is shown in Figure .... x is measured downstream from .... Distances have been normalized on .... Velocities U have .... pressures are presented as coefficients Cp, defined as.... where...." etc.). Next refer to uncertainty estimates for the parameters.
Now describe each of the plots in turn, using a separate paragraph for each. State what each plot shows (e.g. "surface pressure coefficient distributions at two Reynolds numbers compared with a theoretical distribution computed assuming unbounded potential flow"). Mention, and attempt to explain, any imperfections in the experiment revealed by these data (e.g. are the measured distributions symmetrical, is the pressure coefficient at the stagnation point 1). Describe the shapes of the curves. To help in your discussion you can then introduce any auxiliary measurements that have a bearing on the flow (e.g. the unexpected form of the pressure distribution on the cylinder may be partly explained by three-dimensionality in the flow. Figure ?? shows a spanwise profile measured in the cylinder wake at x/D=...").
Make sure your results and discussion include (and justify) the conclusions you want to make and that those conclusions connect with your objectives. Also remember to include any uncertainty estimates in derived results. You should reference a table (copied out of your Excel file) or appendix containing the uncertainty calculation.
Conclusions
Begin this section with one or two sentences summarizing what you did
(e.g." Surface pressure and .... measurements have been made at .... in
...."). Then draw your conclusions which should be numbered, each starting
on a separate line. Most conclusions should be a single sentence that summarizes
an important piece if information which you did not know before the experiment
(and that has already been explained in the Results and Discussion). Make
sure you include conclusions that address the same points as your objectives,
if not, change the objectives.