m![]() +b
+b![]() +kx = f(t)..................(1)
+kx = f(t)..................(1)
A. Borgoltz, W. J. Devenport, S.R. Edwards, and N. Hari
Last revised 7 April 2022
The purpose of this lab period is to apply the digital measurement and analysis capabilities to which you have been introduced to the dynamic beam response experiment you studied earlier using analog instrumentation. A digital-based measurement and control system allows much greater accuracy and flexibility than the analog instrumentation, and also opens up new possibilities for determining or evaluating the dynamic response of this structural system.
You are expected to perform this experiment as you would any of the other experiments in the course. Specifically, you will need to:
Review the chapter on experiment 6, as well as the logbook you and your team(s) generated when performing that experiment using analog instrumentation
Review all the MATLAB programs you have written, and how they might be applied to experiment 6 (see suggestions below)
Carefully read this and the previous chapter of the manual making sure you understand the various techniques for using digital measurement technology.
Meet with the other members of the team in advance to plan for the experiment, and open a logbook to record your preparation. The group will need to decide objectives, which techniques to use, and will need to prepare any required programs, including details of how they will be used during the lab period.
During the experiment you complete the logbook with your experiences, the data you collected, the analysis performed and conclusions drawn. As in the other experiments your grade is based on your logbook, including the preparation you submit electronically before the start of the lab.
As a result of your work in the 3rd and 4th instrumentation lab periods, you should have at least the following two basic data acquisition and analysis programs. We have looked at the a) Time domain code. This code measures two signals simultaneously, graphs them against time, and against each other (as a Lissajous figure) and saves the data if needed. The code calculates and displays the frequencies and amplitudes (HW 3). The code also allows you to control the function generator to sweep through frequencies and determine static flexibility, resonance and natural frequencies and b) Frequency domain code: We have used the spectral analysis to compute the frequency, amplitude and the phase difference of the acquired signals during Instrumentation sessions 3 and 4. You should be comfortable with how to use the code, how to change the sampling rate, how to change the kind of spectrum computed, and how to interpret the spectral values.
Note that these are the minimum needed to re-run experiment 6. You may have been given additional codes and/or an opportunity to program your own enhancements. Such enhancements are greatly encouraged.
The following section details a series of suggestions on how you may use these programs, and the capabilities they provide, to investigate the dynamic response characteristics of the beam structure of experiment 6. In their basic form these programs work with and display voltages. However, we have covered you will need to account for the shaker and proximitor calibrations and how to use their results to calculate the characteristics of the beam system. Note that most strategies for determining the response characteristics will entail using these codes in more than one way. You should also consider combining these strategies with those ideas from the experiment 6 write up, such as varying the mass.
3.1 Time domain code
3.1.1 Rerunning strategies from experiment 6
The time domain code can easily be thought of as a replacement for the oscilloscope
you used the first time you ran experiment 6. With the analog function generator providing
a sinusoidal excitation signal to the structure, the program can be used to display
both the excitation and response and to determine their amplitudes, phases and frequencies.
The difference is that with digital data acquisition the signals can be measured much more accurately,
and examined in much greater detail. The code provides measurements of the amplitude, frequency and phase
(in particular) that are at least an order of magnitude more precise than can be read off an oscilloscope
screen. Since the program can analyze the excitation and response signals, you don’t particularly
need to save the time data acquired for every run.
The additional accuracy is also significant when it comes to designing an experiment to determine the dynamic response characteristics of the beam structure. At the lowest level, you could just repeat the measurements you made with the analog instrumentation and make a comparison. However, it is important to realize that the additional accuracy may make previously impractical measurements perfectly feasible. A good example is measurements of the behavior of the phase response at high and low frequencies. As discussed in section 2 of experiment 6 (see items (f) and (g) following equation 4), the phase response at high and low frequencies compared to the natural frequency has variations that can be used to help estimate the 3 system parameters. Using these asymptotes as part of an analog measurement strategy is difficult because phase lag measurements near 0 and -180 degrees are hard to make using an oscilloscope. With the digital system you have, they are now straightforward. Another example is the high frequency asymptote of the dynamic flexibility (see item (f)), or the low frequency asymptote of the dynamic flexibility (item (a)).
3.2.2 Using impulsive excitation
One important advantage of the time domain code over the analog
instrumentation is that it can be used to record and measure transient behavior.
In other words we can consider solutions to the governing equation of the
structure,
m![]() +b
+b![]() +kx = f(t)..................(1)
+kx = f(t)..................(1)
that involve non-sinusoidal forcing f(t). The simplest
such solution is known as 'free vibration decay'. Free vibration decay occurs
when we give the structure an initial displacement or velocity that starts it
vibrating and we then allow that vibration to decay without applying any force
(i.e. f(t) is zero, but there are initial conditions on x and
![]() ).
).
To get free-vibration decay you first need to turn the shaker coil off, since you don't want to apply any force. You could then create an initial displacement (but no initial velocity) simply by deflecting the beam (say with a finger) and then letting it go. Alternatively, you could create an initial velocity (but no displacement) by gently tapping the undeflected beam with a hard object such as the end of a metal tool (you are effectively applying an impulsive force that gets the beam moving). The second of these two options is generally more practical, since holding the end of the beam steady and releasing it cleanly is not easy.
The solution to equation 1 for impulsive excitation (initial velocity but no displacement) of a lightly damped system is,
where ωn is the (undamped) natural frequency (see experiment 6). ωn and ωd
are almost the same for a lightly damped system, like the beam structure. The
figure below shows a typical impulse response of the type described by equation
2. Using the time domain code it should be
perfectly possible to record an impulse response like this. Set the sampling
rate so you are going to have plenty of points (given the natural frequency of
this system, a few hundred Hz should be sufficient). Set the number of samples
so that you are going to take several seconds of data. Hit the run button and
then, immediately afterwards, tap the beam (this is a two person job). Save the
signals, load them into Excel, and plot the response (the signal from the
proximiter) in the form of the above graph. To do this you will have to
remove the DC offset in the signal (just subtract it), eliminate lots of samples at the start of the signal (recorded before
you tapped the beam), and then restrict your plotting to just a few cycles of
the vibration. Arrange your plot so the initial excursion is in the positive
direction (this may require multiplying the response by -1). With the impulse response in a convenient form
in your logbook, you can now analyze it. First you can get an estimate of the
damped natural frequency (and thus the natural frequency since the two are very
close) from the time period between two successive peaks. Specifically, looking
at equation 2 we will have
ωd = 2p/(t2-t1).
Second, and perhaps most importantly we can relate the rate of decay to the
damping. Specifically, taking the logarithm of Equation 2 we can show that,
where x2/x1 is the ratio of
the amplitudes of two peaks. Since this is a ratio, and since displacement is
proportional to measured voltage, you can calculate this ratio simply as a ratio
of voltage amplitudes. Note that equation 4 does not have to be applied to
consecutive peaks. You can measure the ratio of voltage amplitude over 10
periods and, as long as you use the time for 10 periods in the denominator,
equation 4 should work. The impulse response measurement can therefore give you an
estimate of the natural frequency and, if you already have an estimate of the
mass (say from a set of tone measurements as in section 3.1.1), a low
uncertainty way of determining the damping. The reason that the uncertainty is
low is that you are directly measuring the effect of the damping in controlling
the rate of decay of a vibration. Perhaps the most obvious way to use your frequency domain
program is as a tool for measuring the frequency, amplitude and phase of the
signals generated by sinusoidally exciting the beam structure. However, this is
probably not a good strategy first because it will be a lot less convenient than
using the tone analysis described above and second because it ignores the most
powerful aspect of spectral analysis. Spectral analysis allows us to determine
the amplitude and phase of multiple sinusoidal components of a non-sinusoidal
signal (unlike tone analysis). This can be very useful in rapidly determining
the dynamic response characteristics of a linear system like the beam structure. Consider again the equations derived in experiment 6
for the behavior of the beam structure in response to a sine wave. These give
the ratio between the amplitude of the displacement xm
and the amplitude of the force that produces it fm (the
dynamic flexibility) at an angular
frequency w as
and the phase lag
ym between the
displacement fluctuations and the force fluctuations producing them at angular
frequency ω as
These equations apply not just to a single frequency signals.
They also apply to the individual sinusoidal components of a single non-sinusoidal
signal containing many frequency components. Suppose we were to excite the beam structure with a signal
containing say five frequencies. If we measure the response to this signal we
could then use spectral analysis to separately determine the amplitude and phase
of the response to each of the frequency components. This would also work
for 10 or 100 or any number of frequencies. The ideal excitation signal of this type is an impulse - a short sharp spike
- just like that discussed in section 3.1.2. One can show that such a signal
contains all frequencies with equal amplitude. The response to such a signal therefore also contains all frequencies, but with the amplitudes multiplied by the dynamic
flexibility at each frequency. The amplitude spectrum of this response is thus proportional to the
dynamic flexibility function (equation 5 above). Using spectral
analysis and the right kind of excitation we can therefore, at least in
principle, reveal this entire function in a single measurement. To perform this measurement you will need to record the
response (proximeter) signal. You want to set a sampling rate that implies a frequency
range in the spectrum that is reasonably expected to fit the response function (say a
frequency range of zero to 50Hz). You will need to set the number of samples so that
you are going to take several seconds of data. It is very important that you record
the whole impulse response (until it decays back to zero). You want to set your spectral
analysis to produce amplitude and phase spectra. Since you are expecting to have a response
signal that starts and ends at zero, there is no need to use any windowing, so turn it off.
Tap the beam and click on ‘generate and acquire’ button (this is a two person job). Your
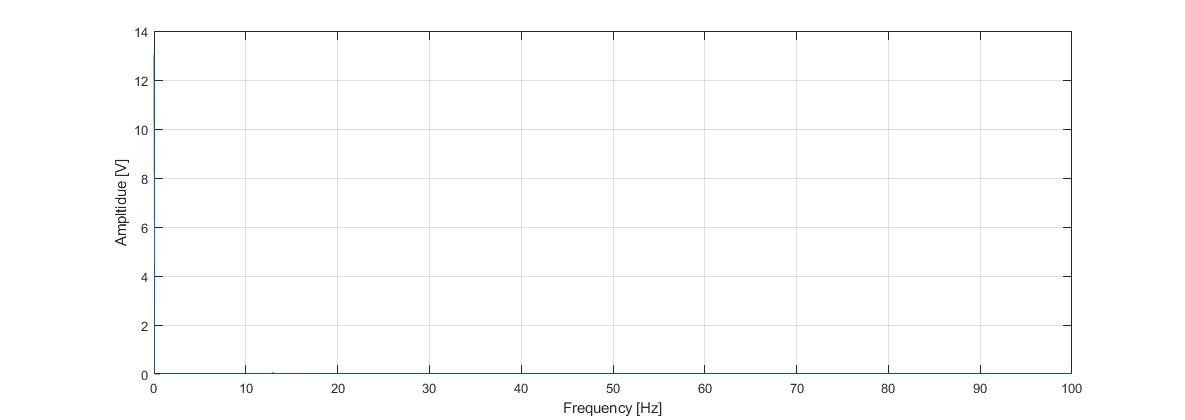
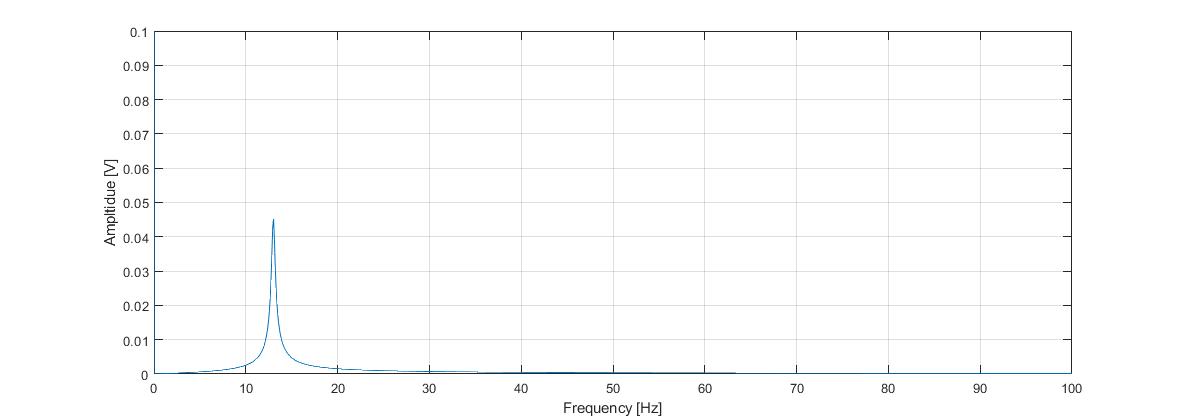
recorded response function should look something like that below. The following figure is typical of the type of amplitude
spectrum you might first see in MATLAB. Note that you may not initially see a large peak in the spectrum. Indeed, the problem is
that the spectrum contains a very large value at zero frequency (associated with
the big DC offset of the proximitor signal), making it hard
to see the rest of the response function. Manually changing the range of the
amplitude axis you should be able to get a clearer picture as shown below: The spectrum you measured is only proportional
to the dynamic flexibility function. However, there is more than one way you can
compare it with equation 5 (which would be an interesting evaluation of the
accuracy of the mathematical model that you could do in your logbook). For
example, you could normalize the measured spectrum on its value at low
frequency, and compare with the equation 5 normalized on the static flexibility
(you can try different values for m, b and k in this
equation to see which best fit the data). Alternatively if you have a separate
measurement (made, say, using the time domain code) of the static flexibility
you can then scale the spectrum to match that value at low frequencies, before
comparing with equation 5. One is to consider averaging the amplitude spectrum measured from several impulses
to reduce the uncertainty. You would want to take square root of the average of the
square of the amplitudes computed from multiple impulses (i.e. RMS averaging). You
can do this by averaging directly in MATLAB using ‘mean’ function. You could also simply analyze the repeatability of each impulse response. Don't forget to include; Objectives A List of Apparatus and Instrumentation Used and the Procedure in
List Form MATLAB codes used and written + description (embed them as
objects) Plots and Tables Showing Your Basic Results Analysis (e.g. comparisons with your analog
instrumentation results). Uncertainty Estimates in Derived Results Conclusions ![]() ..................(2)
..................(2)
![]() ..................(3)
..................(3)
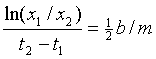 ..................(4)
..................(4)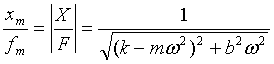 ...........(5)
...........(5)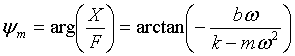 ...........(6)
...........(6)
Include Excel table(s) computing uncertainties in any derived results. It
may not be clear how to do this, particularly for some spectral quantities.
For these quantities a seat-of-the-pants estimate is fine.
In list form